Code And Fun

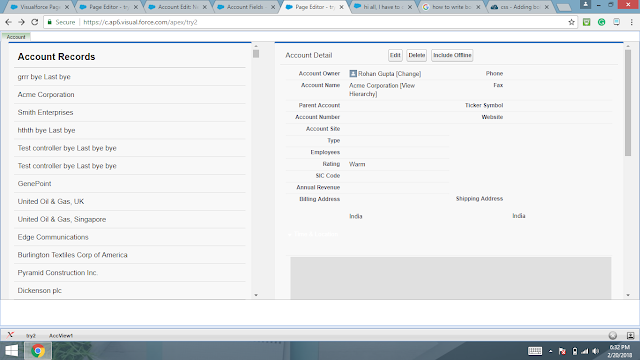
In this post, I am going to tell you how to use  Standard Object and Extensions in a visualforce page. Task:  When you click on an Account's record, it will display the fields data of selected record. First of all, I am going to design a visualforce page look like this. Function: We create a tab whose name is Account . It has two part one is Account Records and another is Account Detail as shown in the figure. In Account Records section, we display all records of the Account object. In Account Details section, we display the details of the selected Account's record. Source code: Visualforce page <apex:page showHeader="false" sidebar="false" standardController="Account" extensions="AccView1">     <link rel="stylesheet" href="https://maxcdn.bootstrapcdn.com/bootstrap/3.3.7/css/bootstrap.min.css"/>     <script src="https://ajax.googleapis.com/ajax/libs/jquery/3.3....

Profile: A profile is a collection/group of settings and permissions that define what a user can do in Salesforce. A profile controls Object permissions, Field permissions, User permissions, Tab settings, Apex class access, Page Layouts, App settings, Visualforce page access, Record types, Login hours, and login IP ranges.   A profile can be assigned to many users, but a user can be assigned a single profile at a time. Types of profiles: Standard Profiles: By default, salesforce provides below standard profiles. We cannot delete standard ones like  Read Only, Standard User, Marketing User, System Administrator etc. Each of these standard ones includes a default set of permission for all of the standard object available on the platform. Custom Profiles: Custom ones defined by us. They can be deleted if there are no users assigned to that particular one. How to create Profiles in Salesforce: 1. Go to Setup .  2. Search for profiles in Quick Find...

Merge Sort is a Divide and Conquer algorithm. It divides the input array into two halves and then merges the two sorted halves. Algorithm: MergeSort(a[], l, r) If r > l Find the middle point to divide the array into two halves: middle m = (l+r)/2 . Call mergeSort for the first half: Call mergeSort(a, l, m) . Call mergeSort for the second half: Call mergeSort(a, m+1, r) . Merge the two halves sorted in step 2 and 3: Call merge(a, l, m, r) . The following diagram: Source code in Java: class MergeSort {      // Merge two subarray of a[].      // First subarray is a[l...m].     //  Second subarray is a[m+1....r].       void merge(int a[], int l, int m, int r)    {         int n1 = m-l+1;         int n2 = r-m;         // Create temp array.         int L[] = new int[n1];   ...

Source code in Java: public class Demo {         public static void main(String arg[])         {                   String s = " good23bad4 ";                   int sum = 0;                   for (char c : s.toCharArray())                   {                          if (Character.isDigit(c))                           {                                sum += Character.getNumericValue(c);                          }             ...

A disjoint-set data structure is a data structure that keeps track of a set of elements partitioned into a number of non-overlapping subsets. Union-Find Algorithm is an algorithm which performs two operations: Find: Determine which subset a particular element is in. Union: Join two subsets into a single subset.   Source code in java import java.util.*; import java.lang.*; import java.io.*; class Graph { int V, E; // V-> no. of vertices & E->no.of edges Edge edge[]; // /collection of all edges class Edge { int src, dest; }; // Creates a graph with V vertices and E edges Graph(int v,int e) { V = v; E = e; edge = new Edge[E]; for (int i=0; i<e; ++i) edge[i] = new Edge(); } // A utility function to find the subset of an element i int find(int parent[], int i) { if (parent[i] == -1) return i; return find(parent, parent[i]); } // A uti...

Spanning tree of a graph is a subgraph that contains all the vertices and is also a tree.  A minimum spanning tree of an undirected graph G is a tree formed from graph edges that connected all the vertices of G with minimum total cost (weights). A minimum spanning tree exists only if the graph is connected. In this post, O(ELogV) algorithm for adjacency list representation is discussed. Prim's Algorithm:  STEP 1: Create an array parent[] of size V and initialize with -1. STEP 2: Create a min heap (or Priority queue) of size V . Let the min heap be h . STEP 3: Insert all vertices into h such that the key value of starting vertex is 0 and the key value of other vertices is infinite. STEP 4: While h is not empty.      a) u = extractMin() from h .      b) for every adjacent v of u .            if v is in h .               i) update key value of v...

BFS algorithm works similar to level-order traversal of the tree.   BFS also uses queues.   Initially, BFS starts at a given vertex, which is at level 0.   In the first stage, it visits all vertices at level 1.   In the second stage, it visits all vertices at level 2. Source code in Java: import java.util.LinkedList; import java.util.Iterator; /**  *  * @author Rohan  */ public class Graph  {     private int V;   // No. of vertices     // Array  of lists for Adjacency List Representation     private LinkedList<Integer> adj[];     // Constructor     Graph(int v)     {         V = v;         adj = new LinkedList[v];         for (int i=0; i<v; ++i)             adj[i] = new LinkedList();     } ...