AVL Tree Rotations
Rotations
When the tree structure changes, we need to modify the tree to restore the AVL tree property. This can be done using single or double rotations.
Types of Violations
Let us assume the node that must be rebalanced in X. Violations might occur in four cases:
When the tree structure changes, we need to modify the tree to restore the AVL tree property. This can be done using single or double rotations.
Types of Violations
Let us assume the node that must be rebalanced in X. Violations might occur in four cases:
- Insertion into the left subtree of the left child of X.
- Insertion into the right subtree of the right child of X.
- Insertion into the right subtree of the left child of X.
- Insertion into the left subtree of the right child of X.
Single Rotation
Left Left Rotation (LL Rotation) [Case 1]:
Rotation does not have to be done at the root of a tree. In general, we start at the node inserted and travel up the tree, updating the balance information at every node on the path.

AVLTree y = x.right;
// Perform rotation
y.left = x;
x.right = y.left;
// Update heights
x.height = max(height(x.left), height(x.right)) + 1;
y.height = max(height(y.left), height(y.right)) + 1;
// Return new root
return y;
}
Right Right Rotation (RR Rotation) [Case 2]:
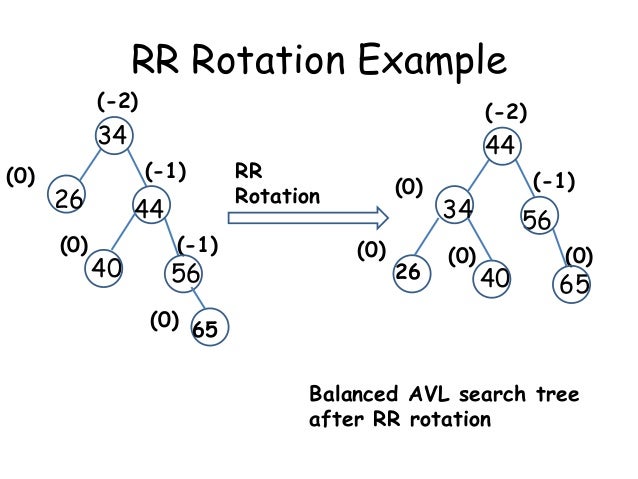
AVLTree x = y.left;
// Perform rotation
x.right = y;
y.left = x.right;
// Update heights
y.height = Math.max(height(y.left), height(y.right)) + 1;
x.height = Math.max(height(x.left), height(x.right)) + 1;
return x;
}
Left Right Rotation (LR Rotation) [Case 4]:
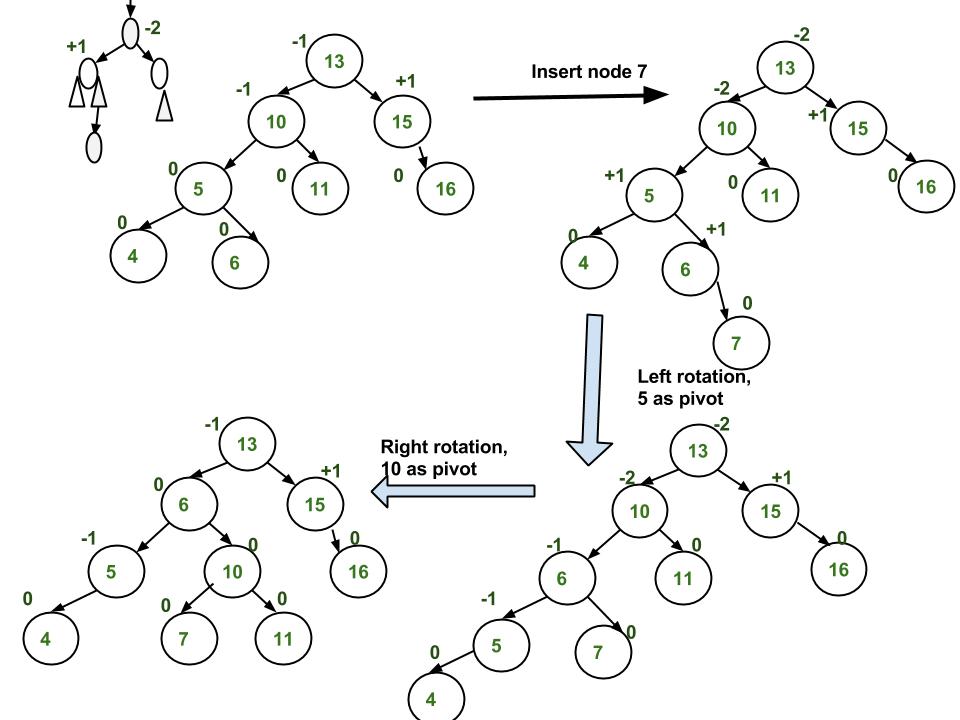

public AVLTree rotateLeft (AVLTree x) {AVLTree y = x.right;
// Perform rotation
y.left = x;
x.right = y.left;
// Update heights
x.height = max(height(x.left), height(x.right)) + 1;
y.height = max(height(y.left), height(y.right)) + 1;
// Return new root
return y;
}
Right Right Rotation (RR Rotation) [Case 2]:

public AVLTree rightRotate(AVLTree y) {AVLTree x = y.left;
// Perform rotation
x.right = y;
y.left = x.right;
// Update heights
y.height = Math.max(height(y.left), height(y.right)) + 1;
x.height = Math.max(height(x.left), height(x.right)) + 1;
return x;
}
Left Right Rotation (LR Rotation) [Case 4]:

public AVLTree lRRotate(AVLTree z) {
z.left = rotateLeft(z.left);
return rotateRight(z);
}
Right Left Rotation (RL Rotation) [Case 3]:
public AVLTree rLRotate(AVLTree z) {
z.right= rotateRight(z.right);
return rotateLeft(z);
}


Comments
Post a Comment